Mathematics 2017 JAMB Past Questions

1. Given T = { even numbers from 1 to 12 }

N = {common factors of 6, 8 and 12}
Find T ∩ N

A. {2, 3}
B. {2, 3, 4}
C. {3, 4, 6}
D. {2}

Correct Answer: Option D

Explanation

T = {evenn numbers from 1 to 12}
N = {common factors of 6,8 and 12}
Find T ∩ N
T = {2, 4, 6, 8, 10, 12}
N = {2}
T ∩ N = {2} i.e value common to T & N

2.What is the next number in the series 2, 1,

\frac{1}{2}

\frac{1}{4}

...

A. $\frac{1}{3}$

B. $\frac{2}{8}$
C. $\frac{3}{7}$
D. $\frac{1}{8}$

Correct Answer: Option D

Explanation

2, 1,

\frac{1}{2}

\frac{1}{4}

.....

There are 4 terms in the series
Therefore the next number will be the 5th term

T_n = ar

^{n - 1}

(formular for geometric series)

a = first term = 2

r = common rate =

\frac{next term}{previous term}

\frac{1}{2}

n = number of terms

T₅ = 5th term = ?

T₅ = ar

^{5 - 1}

= ar

^{4}

= 2 × (ar

^{n - 1}

)⁴

= 2 ×

\frac{1}{16}

\frac{1}{8}

3. If U = {x : x is an integer and 1 ≤ x ≤ 20 }

E1 = {x: x is a multiple of 3}
E2 = {x: x is a multiple of 4} and an integer is picked at random from U, find the probability that it is not in E2

A. $\frac{3}{4}$

B. $\frac{3}{10}$
C. $\frac{1}{4}$
D. $\frac{1}{20}$

Correct Answer: Option A

Explanation

U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}

E1 = {3, 6, 9, 12, 15, 18}

E2 = {4, 8, 12, 16, 20}

Probability of E2 =

\frac{5}{20}

i.e

\frac{Total number in E_{2}}{Entire number in set}

Probability of set E2 = 1 −

\frac{5}{20}

\frac{15}{20}

\frac{3}{4}

4.The curved surface area of a cylinder 5cm high is 110cm². Find the radius of its base

π =

\frac{22}{7}

A. 2.6cm
B. 3.5cm
C. 3.6cm
D. 7.0cm

Correct Answer: Option B

Explanation

Curved surface area of cylinder = 2πrh

110 = 2 ×

\frac{22}{7}

× r × 5

r =

\frac{110 \times 7}{44 \times 5}

= 3.5cm

5. If two graphs Y = px² + q and y = 2x² − 1 intersect at x =2, find the value of p in terms of q

A. q − $\frac{8}{7}$

B. 7 − $\frac{q}{4}$
C. 8 − $\frac{q}{2}$
D. 7 +

Correct Answer: Option B

Explanation
Y = Px² + q

Y = 2x² - 1

Px² + q = 2x² - 1

Px² = 2x² - 1 - q

p = $\frac{2 x^{2} - 1 - q}{x^{2}}$

at x = 2

P =

=

=

P =
- B. √3 − $\frac{1}{2}$
- C. $\frac{1}{2}$ √2
- D. 1 + $\frac{\sqrt{2}}{2}$
- B. -1
- C. 1
- D. $\frac{π}{2}$
- D. 3 $\frac{2}{3}$
- B. $\frac{N^{2} S L}{M^{2}}$
- C. $\frac{N^{2} S L}{M}$
- D. $\frac{N S L}{M^{2}}$
Correct Answer: Option B

Explanation
M = N
,

make T subject of formula square both sides

M =

TM = NSL

T =

11.Simplify 3 $^{n - 1}$ × $\frac{27^{n + 1}}{81^{n}}$
A. 3 $^{2 n}$

B. 9

C. 3ⁿ

D. 3

^{n + 1}

Correct Answer: Option B

Explanation

^{n - 1}

\frac{27^{n + 1}}{81^{n}}

= 3

^{n - 1}

\frac{3^{3 (n + 1)}}{3^{4 n}}

= 3

^{n - 1 + 3 n + 3 - 4 n}

= 3

^{4 n - 4 n - 1 + 3}

3^{2}

= 9

12.The locus of a point which is equidistant from the line PQ forms a

A. circle centre P
B. pair of parallel lines each opposite to PQ
C. circle centre Q
D. perpendicular line to PQ

Correct Answer: Option D

Explanation

The locus of points at a fixed distance from the point P is a circle with the given P at its centre.

The locus of points at a fixed distance from the point Q is a circle with the given point Q at its centre

The locus of points equidistant from two points P and Q i.e line PQ is the perpendicular bisector of the segment determined by the points

Hence, The locus of a point which is equidistant from the line PQ forms a perpendicular line to PQ

13.Given T = {even numbers from 1 to 12}

N = {common factors of 6, 8 and 12} Find T n N

A. {2, 3}
B. {2, 3, 4}
C. {3, 4, 6}
D. {2}

Correct Answer: Option D

Explanation

Given T = {even numbers from 1 to 12}
= { 2, 4, 6, 8,10, 12}

N = {common factors of 6, 8 and 12}

= {2} Find T n N = {2}

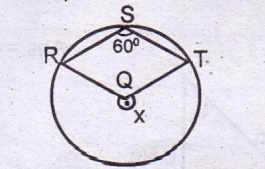
Given the quadrilateral RSTO inscribed in the circle with O as centre. Find the size angle x and given RST = 60^o

A. 100^o
B. 140^o
C. 120^o
D. 10^o $\frac{7 - q}{4}$ $\frac{7 - q}{4}$ $\frac{7 - q}{4}$

Correct Answer: Option C

Explanation
If RST = 60^o

RXT = 2 × RST

(angle at the centre twice angle at the circumference)

RXT = 2 × 60

= 120^o

15. Find the sum of the range and the mode of the set of numbers 10, 9, 10, 9, 8, 7, 7, 10, 8, 10, 8, 4, 6, 9, 10, 9, 7, 10, 6, 5
A. 16
B. 14
C. 12
D. 10

Correct Answer: Option A

Explanation

Range = Highest Number - Lowest Number

Mode is the number with highest occurrence
10, 9, 10, 9, 8, 7, 7, 10, 8, 4, 6,, 9, 10, 9, 7, 10, 6, 5

Range = 10 − 4 = 6

Mode = 10

Sum of range and mode = range + mode = 6 + 10

= 16

16. Find the sum to infinity of the series

\frac{1}{4}

\frac{1}{8}

\frac{1}{16}

,..........

A. $\frac{1}{2}$

\frac{3}{5}

\frac{- 1}{5}

\frac{73}{12}

Correct Answer: Option A

Explanation

Sum to infinity

∑ = arn − 1

=

\frac{a}{1}

− r

a =

\frac{1}{4}

r =

\frac{1}{8}

\frac{1}{4}

r =

\frac{1}{s}

\frac{4}{1}

\frac{1}{2}

S =

\frac{1 \div 4}{1}

−

\frac{1}{2}

\frac{1}{4}

\frac{1}{2}

\frac{1}{4}

\frac{2}{1}

\frac{1}{2}

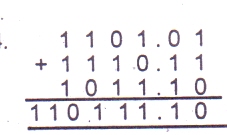
The base in which the operation was performed was

A. 6
B. 2
C. 4
D. 5

Correct Answer: Option B

18.The value of x + x ( xx) when x = 2 is

A. 16
B. 10
C. 18
D. 24

Correct Answer: Option B

Explanation

when x=2, we have

2 + 2 (2^{2})

2 + 8 = 10

19. In a regular polygon, each interior angle doubles its corresponding exterior angle. Find the number of sides of the polygon

A. 8
B. 6
C. 4
D. 3

Correct Answer: Option B

Explanation

2x + x = 180^o

3x = 180^o

x = 60^o (exterior angle of the polygon)

angle =

\frac{total angle}{number of sides}

60 =

\frac{360}{n}

n =

\frac{360}{60}

n = 6 sides

20. A cylindrical tank has a capacity of 3080m³. What is the depth of the tank if the diameter of its base is 14m? Take pi = 22/7.

A. 23m
B. 25m
C. 20m
D. 22m

Correct Answer: Option C

Explanation

Capacity = Volume = 3080m³

base diameter = 14m

radius =

\frac{diameter}{2}

= 7m

Volume of Cylidner = Capacity of cylinder

πr²h = 3080

\frac{22}{7}

× 7 × 7 × h = 3080

h =

\frac{3080}{22 \times 7}

h = 20m

21. Simplify 4

\sqrt{27}

+ 5

\sqrt{12}

− 3

\sqrt{75}

A. 7
B. − 7
C. − 7 $\sqrt{3}$

D. 7

\sqrt{3}

Correct Answer: Option D

Explanation

\sqrt{27}

+ 5

\sqrt{12}

− 3

\sqrt{75}

= 4

\sqrt{3}

× 9 + 5

\sqrt{3}

× 4 − 3

\sqrt{3}

× 25

= 4 × 3

\sqrt{3}

+ 5 × 2

\sqrt{3}

− 3 × 5

\sqrt{3}

= 12

\sqrt{3}

+ 10

\sqrt{3}

− 15

\sqrt{3}

= (12 + 10 − 15)

\sqrt{3}

= 7

\sqrt{3}

22.A man covered a distance of 50 miles on his first trip, on a later trip he traveled 300 miles while going 3 times as fast. His new time compared with the old distance was?

A. three times as much
B. the same
C. twice as much
D. half as much

Correct Answer: Option C

Explanation

Let the speed of the 1st trip be x miles/hr

and the speed of the 2nd trip be 3x miles/hr

Speed = distance/time

∴ Time taken to cover a distance of 50 miles on the 1st trip

=

\frac{50}{x h r}

time taken to cover a distance of 300 miles on the next trip

=

\frac{300}{3 x h r}

\frac{100}{x h r}

∴the new time compared with the old time is twice as much

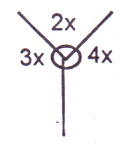
In the figure, find x

A. 40^o
B. 55^o
C. 50^o
D. 60^o

Correct Answer: Option A

Explanation

Sum of angle at a point = 360^o

2x + 3x + 4x = 360

9x = 360

x =

\frac{360}{9}

x = 40^o

24. Divide 4x3 - 3x + 1 by 2x - 1

A. 2x² -x + 1
B. 2x² - x -1
C. 2x² + x + 1
D. 2x² + x -1

Correct Answer: Option D

Explanation

by method of long division, we get the answer.

25. A car dealer bought a second-hand car for of 250,000 and spent N 70,000 refurbishing it. He then sold the car for N400,000. What is the percentage gain?

A. 60%
B. 32%
C. 25%
D. 20%

Correct Answer: Option C

Explanation

Total Cost Price = N(250,000 + 70,000)

= N 32,000

Selling Price = N 400,000(Given)

Gain = Selling Price - Cost Price

= 400,000 - 300,000

= 80,000

% gain =

\frac{Gain}{Cost Price}

× 100

=

\frac{80, 000}{320, 000}

× 100

Gain % = 25%

26. Find the number of ways that the letters of the word EXCELLENCE be arranged

A. $\frac{10!}{2! 2! 2!}$

\frac{10!}{4! 2!}

\frac{10!}{4! 2! 2!}

\frac{10!}{2! 2!}

Correct Answer: Option C

Explanation

EXCELLENCE

It is a ten letter word = 10!

Since we have repeating letters, we have to divide to remove the duplicates accordingly. There are 4 Es, 2 Cs, 2 Ls

∴ there are

\frac{10!}{4! 2! 2!}

ways to arrange

27. Evaluate

\frac{0.00000231}{0.007}

and leave the answer in standard form

A. 3.3 x 10^-4
B. 3.3 x 10^-3
C. 3.3 x 10^-5
D. 3.3 x 10^-8

Correct Answer: Option A

Explanation

\frac{0.00000231}{0.007}

to standard form

=

\frac{231 \times 10^{- 8}}{7 \times 10^{- 3}}

= 33 × 10

^{- 8 - (- 3)}

= 33 × 10

^{- 8 + 3}

= 33 × 10-5
= 3.3 x 10^-4

28.If a rod 10cm in length was measured as 10.5cm, calculate the percentage error

A. 5%
B. 10%
C. 8%
D. 7%

Correct Answer: Option A

Explanation

Actual measurement = 10cm

approximated value of measurement = 10.5cm

% error =

\frac{Actual measurement − Approximated}{Actual measure}

× 100

=

\frac{10 - 10.5}{10}

× 100

=

\frac{- 0.5}{10}

× 100

ignore -sign i.e take absolute value

=

\frac{0.5}{10}

× 100

= 5 %

29. Find the principal which amounts to ₦ 5,500 at a simple interest in 5 years at 2% per annum

A. ₦ 4,900
B. ₦ 5,000
C. ₦ 4,700
D. ₦ 4,000

Correct Answer: Option B

Explanation

Principal = P, Simple Interest = I, Amount = A

Amount = Principal + Simple Interest

I =

\frac{P R T}{100}

R = rate, T = time

I =

\frac{P \times 5 \times 2}{100}

I =

\frac{10 P}{100}

I =

\frac{P}{10}

Amount A = P + I

5500 = P +

\frac{P}{10}

Multiply through by 100

5500 = 10P + P

5500 = 11P

p =

\frac{5500}{11}

p = ₦5000

30.

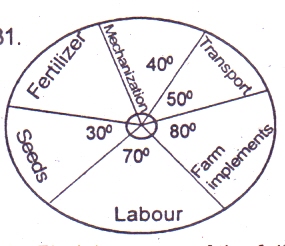
The pie chart shows the allocation of money to each sector in a farm. The total amount allocated to the farm is ₦ 80 000. Find the amount allocated to fertilizer

A. ₦ 35, 000
B. ₦ 40,000
C. ₦ 25,000
D. ₦ 20,000

Correct Answer: Option D

Explanation

Total angle at a point = 3600

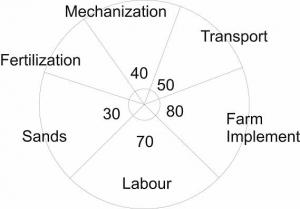
∴ To get the angle occupied by fertilizer we have,

40 + 50 + 80 + 70 + 30 + fertilizer(x) = 360

270 + x = 360

x = 360 - 270

x = 90

Total amount allocated to the farm
= ₦ 80,000

∴Amount allocated to the fertilizer

=

\frac{fertilizer (angle) × Total amount}{total angle}

\frac{90}{360}

× 80,000

= ₦20,000

31. In how many ways can the word MATHEMATICS be arranged?

A. $\frac{11!}{9! 2!}$

\frac{11!}{9! 2! 2!}

\frac{11!}{2! 2! 2!}

\frac{11!}{2! 2!}

Correct Answer: Option C

Explanation

MATHEMATICS is an eleven letter word = 11!

There are 2Ms and 2As and 2Es

Divide the number of repeating letters

=

\frac{11!}{2! 2! 2!}

32. In how many ways can the word MACICITA be arranged?

A. $\frac{8!}{2!}$

\frac{8!}{3! 2!}

\frac{8!}{2! 2! 2!}

D. 8!

Correct Answer: Option C

Explanation

MACICITA is an eight letter word = 8!

Since we have repeating letters, we have to divide to remove duplicates accordingly. There are 2A, 2C, 2I

∴

\frac{8!}{2! 2! 2!}

33. y is inversely proportional to x and y and 6 when x = 7. Find the constant of the variation

A. 47
B. 42
C. 54
D. 46

Correct Answer: Option B

Explanation

Y ∝

\frac{1}{2}

Y = 6, X = 7

Y =

\frac{k}{x}

where k is constant

6 =

\frac{k}{7}

k = 42

In the diagram MN, PQ and RS are parallel lines. What is the value of the angle marked X?

A. 123^o
B. 170^o
C. 117^o
D. 137^o

Correct Answer: Option C

Explanation

MN || PQ || RS

MN = PQ = RS (parallel lines)

Label the angle in the lines

a = i (corresponding angles are equal)

b = x (corresponding angles are equal)

If |MN| = |RS|

If a = i

and a = 63 = i

a + b = 180 (Adjacent interior angles are supplementary i.e add to 180)

∴ i + x = 180

63 + x = 180

x = 180 - 63

x = 1170

35.Find the equation of the locus of a point p (x, y) such that pv = pw, where v= (1, 1) and w = (3, 5)

A. 2x + 2y = 9
B. 2x + 3y = 8
C. 2x + y = 9
D. x + 2y = 8

Correct Answer: Option D

Explanation

The locus of a point p(x, y) such that pv = pw where v = (1, 1)

and w = (3, 5). This means that the point p moves so that its distance from v and w are equidistance

\sqrt{(x - x_{1})^{2} + (y - y_{1})^{2}}

\sqrt{(x - x_{2})^{2} + (y - y_{2})^{2}}

\sqrt{(x - 1)^{2} + (y - 1)^{2}}

\sqrt{(x - 3)^{2} + (y - 5)^{2}}

square both sides
(x - 1)² + (y - 1)² = (x - 3)² + (y - 5)²

x² - 2x + 1 + y2 - 2y + 1 = x² - 6x + 9 + y2 - 10y + 25

x² + y² -2x -2y + 2 = x² + y² - 6x - 10y + 34

Collecting like terms
x² - x² + y² - y² - 2x + 6x -2y + 10y = 34 - 2

4x + 8y = 32

Divide through by 4

x + 2y = 8

36. Find ∫(x² + 3x − 5)dx

\frac{x_{3}}{3}

\frac{3 x_{2}}{2}

- 5x + k

\frac{x_{3}}{3}

\frac{3 x_{2}}{2}

+ 5x + k

\frac{x_{3}}{3}

\frac{3 x_{2}}{2}

- 5x + k

\frac{x_{3}}{3}

\frac{3 x_{2}}{2}

+ 5x + k

37.In the diagram below MN is a chord of a circle KMN centre O and radius 10cm. If

- A. 10cm
- B. 18cm
- C. 17cm
- D. 12cm
Correct Answer: Option A

Explanation

Find the diagram
Sin 70^o

x = 10 Sin 70^o

= 9.3969

Hence, length of chord MN = 2x

= 2 × 9.3969

= 18.79

= 19cm (nearest cm)
38. If m * n = [m_n − n_m] for m, n belong to R, evaluate − 3 * 4
- A. 3
- B. 4
- C. 5
- D. 6
Correct Answer: Option C

Explanation
m * n = -

m = − 3

n = 4

∴ − 3 × 4 = -

=

=

=
39. Factorize completely x2 + 12xy + y2 + 3x + 3y - 18
- A. (x + y + 6)(x + y -3)
- B. (x - y - 6)(x - y + 3)
- C. (x - y + 6)(x - y - 3)
- D. (x + y - 6)(x + y + 3)
Correct Answer: Option A

Explanation
$x^{2} + 2 x y + y^{2} + 3 x + 3 y - 18$

$x^{2} + 2 x y + 3 x + y^{2} + 3 y - 18$

$x^{2} + 2 x y - 3 x + 6 x + y^{2} - 3 y + 6 y - 18$

$x^{2} + 2 x y - 3 x + y^{2} - 3 y + 6 x + 6 y - 18$

$x^{2} + x y - 3 x + x y + y^{2} - 3 y + 6 x + 6 y - 18$

x(x + y - 3) + y(x + y - 3) + 6(x + y - 3)

= (x + y - 3)(x + y + 6)

= (x + y + 6)(x + y -3)

40. Make S the subject of the relation

p = s + $\frac{s m^{2}}{n r}$
- A. s = $\frac{n r p}{n r + m^{2}}$
B. s = nr + $\frac{m^{2}}{m r p}$
C. s = $\frac{n r p}{m r}$ + m²
^{D.
s = $\frac{n r p}{n r}$ + m²} Correct Answer: Option A
Explanation
p = s + $\frac{s m^{2}}{n r}$

p = s + ( 1 + $\frac{m^{2}}{n r}$ )

p = s (1 + $\frac{n r + m^{2}}{n r}$ )

nr × p = s (nr + m2)

s = $\frac{n r p}{n r + m^{2}}$

41. The operation * on the set R of real number is defined by x * y = 3x + 2y − 1, find 3*− 1

A. 9
B. - 9
C. 6
D. - 6

Correct Answer: Option C

Explanation

x * y is an operation on 3x + 2y − 1

Find 3A − 1

x = 3, y = −1

3 * − 1 on 3x + 2y − 1

3(3) + 2(−1) −1

= 9 − 2 − 1

= 6

42. Find the gradient of the line joining the points (3, 2) and (1, 4)

A. 3/2
B. 2/1
C. -1
D. 3/2

Correct Answer: Option C

Explanation

Gradient of line joining points (3, 2), (1, 4)

Gradient =

\frac{Change in Y}{Change in X}

\frac{y_{2} - Y_{1}}{x_{2} - x_{1}}

\)

(X1, Y1) = (3, 2)

(X2, Y2) = (1, 4)

Gradient =

\frac{4 - 2}{1 + 3}

\frac{2}{- 2}

= −1

43. Simplify (3√64a³)

^{- 1}

A. 4a
B. $\frac{1}{8 a}$

C. 8a
D. $\frac{1}{4 a}$

Correct Answer: Option D

Explanation

(3√64a³)

^{- 1}

\frac{1}{(3√64a^3)  = \(\frac{1}{4a}

44. If

\frac{2 \sqrt{3} - \sqrt{2}}{\sqrt{3} + 2 \sqrt{2}}

= m + n √ 6,

44. find the values of m and n respectively

A. 1, − 2
B. − 2, n = 1
C. $\frac{- 2}{5}$ , 1
D. $\frac{2}{3}$ $\frac{2}{3}$
Correct Answer: Option B

Explanation
$\frac{2 \sqrt{3} - \sqrt{2}}{\sqrt{3} + 2 \sqrt{2}}$ = m + n√6

$\frac{2 \sqrt{3} - \sqrt{2}}{\sqrt{3} + 2 \sqrt{2}}$ x $\frac{\sqrt{3} - 2 \sqrt{2}}{\sqrt{3} - \sqrt{2}}$

$\frac{2 \sqrt{3} (\sqrt{3} - 2 \sqrt{2}) - \sqrt{2} (\sqrt{3} - 2 \sqrt{2})}{\sqrt{3} (\sqrt{3} - 2 \sqrt{2}) + 2 \sqrt{2} (\sqrt{3} - 2 \sqrt{2})}$

$\frac{2 \times 3 - 4 \sqrt{6} - 6 + 2 \times 2}{3 - 2 \sqrt{6} + 2 \sqrt{6} - 4 \times 2}$

= $\frac{6 - 4 \sqrt{6} - \sqrt{6} + 4}{3 - 8}$

= $\frac{0 - 4 \sqrt{6} - 6}{5}$

= $\frac{10 - 5 \sqrt{6}}{5}$

= − 2 + √6

∴ m + n $\sqrt{6}$ = − 2 + √6

m = − 2, n = 1 $\frac{2}{3}$ $\frac{2}{3}$

\frac{2}{3}

45. If α and β are the roots of the equation 3x² + bx − 2 = 0. Find the value of

\frac{1}{α}

\frac{1}{β}

A. $\frac{- 5}{3}$

B. $\frac{- 2}{3}$
C. $\frac{1}{2}$
D. $\frac{5}{2}$

Correct Answer: Option D

Explanation

\frac{1}{α}

\frac{1}{β}

\frac{β - α}{α β}

3x² + 5x + 5x − 2 = 0.

Sum of root = α + β

Product of root = αβ

x² +

\frac{5 x}{3}

−

\frac{2}{3}

= 0

αβ = −

\frac{- 2}{3}

α + β =

\frac{5}{3}

∴

\frac{α + β}{α β}

= −

\frac{\frac{5}{3}}{\frac{2}{3}}}

= −

\frac{2}{3}

\frac{3}{3}

\frac{5}{2}

\frac{5}{2}

\frac{5}{2}

\frac{5}{2}

\frac{5}{2}

46 . Find the range of the following set of numbers 0.4, −0.4, 0.3, 0.47, −0.53, 0.2 and −0.2

A. 1.03
B. 0.07
C. 0.03
D. 1.0

Correct Answer: Option D

Explanation

0.4, −0.4, 0.3, 0.47, −0.53, 0.2, −0.2

Range is the difference between the highest and lowest value

i.e Highest − Lowest

− 0.53, −0.4, −0.2, 0.2, 0.3, 0.4, 0.47

0.47 is the highest

− 0.53 is the lowest

∴ = 0.47 − (− 0.53)

∴0.47 + 0.53

= 1.0

47. Evaluate 1 − (

\frac{1}{5}

+ 1

\frac{2}{3}

) + (5 + 1

\frac{2}{3}

)

A. 4
B. 3
C. 2 $\frac{2}{3}$ $\frac{2}{3}$ $\frac{2}{3}$

D. 3

\frac{2}{3}

Correct Answer: Option D

Explanation

1 − (

\frac{1}{5}

+ 1

\frac{2}{3}

) + (5 + 1

\frac{2}{3}

)

1 − (

\frac{1}{5}

\frac{5}{3}

) + (5 +

\frac{5}{3}

)

1 −

\frac{1}{3}

\frac{20}{3}

\frac{22}{3}

48. What is the product of 2x² − x + 1 and 3 − 2x

A. 4x³ − 8x² + 5x + 3
B. −4x³ + 8x² − 5x + 3
C. −4x³ − 8x² + 5x + 3
D. 4x³ + 8x² − 5x + 3

Correct Answer: Option B

Explanation

(2x² - x + 1) × (3 - 2x);

3(2x² - x + 1) - 2x (2x² - x + 1)

6x² - 3x + 3 - 4x³ + 2x² - 2x

-4x³ + 8x² -5x + 3

\frac{5}{2}