Mathematics 2018 JAMB Past Questions
Mathematics 2018 JAMB Past Questions
1.In a class
of 40 students, 32 offer Mathematics, 24 offer Physics and 4 offer
neither Mathematics nor Physics. How many offer both Mathematics and
Physics?
- A. 4
- B. 8
- C. 16
- D. 20
2.Find the values of x for which
- < 4
- A. x < 8
- B. x > -6
- C. x < 4
- D. x > -3
3


Find \N\
- A. 65
- B. 23
- C. 17
- D. 91
4. If X, Y can take values from the set (1, 2, 3 ,4), find the probability that the product of X and Y is not greater than 6
- A.
Correct Answer: Option C
Explanation

Pr(product of x and y NOT > 6 ) =
=
5
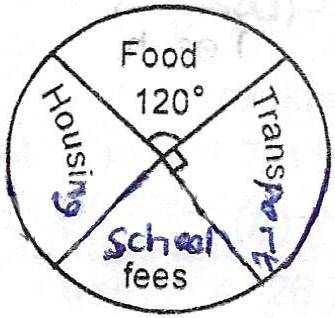
The pie chart shows the monthly
expenditure of a public servant. The monthly expenditure on housing is
twice that of school fees. How much does the worker spend on housing if
his monthly income is N7200?
- A. 1000
- B. 2000
- C. 3000
- D. 4000
- A. 8
- A.
- B. 1
- C.
- A. 7
- B. 6
- C. 5
- D. 4
- A. 1110
- B. 10111
- C. 11101
- D. 111100
- A. 10°
- B. 28°
- C. 36°
- D. 40°
- A.
- B.
- C. 5
- D. 9
6. Evaluate 5log x 2
Correct Answer: Option B
7. A trader realises 10x - x
Naira profit from the sale of x bags of corn. How many bags will give him the maximum profit?
Correct Answer: Option C
Maximum profit can be achieved when the differential of profit with respect to number of bags(x) is 0
i.e.
= 0
= 10 - 2x = 0
10 = 2x
Then x =
= 5
Answer is C
Explanation
Profit (P) = 10 − 2
Maximum profit can be achieved when the differential of profit with respect to number of bags(x) is 0
i.e.
= 0
= 10 - 2x = 0
10 = 2x
Then x =
= 5
Answer is C
8. If y = 23
, find y, leaving your answer in base two
Correct Answer: Option B
9
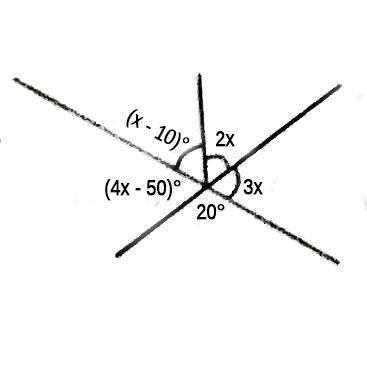
Correct Answer: Option D
x - 10 + 4x - 50 + 2x + 3x + 20 = 360
10x - 40 = 360
10x = 360 + 40
10x = 400
x =
x = 40
Explanation
The diagram shows angles at a point, the total angle at a point is 360x - 10 + 4x - 50 + 2x + 3x + 20 = 360
10x - 40 = 360
10x = 360 + 40
10x = 400
x =
10. Solve for t in the equation t + (21 - t) = 11
Explanation
t + (21 - t) = 11Multiply through by the LCM of 4 and 3 which is 12
12 x(t) + 12 x (
(21 - t)) = (11 x 12)
9t + 4(21 - t) = 132
9t + 84 - 4t = 132
5t + 84 = 132
5t = 132 - 84 = 48
t =
t = 9
Answer is D
- A.
- B.
- C.
- D.
- A.
- B.
11. A school girl spends of her pocket money on books and
on dress. What fraction remains?
Correct Answer: Option C
12. If + = 1. Make y the subject of the relation.
- C.
- D.
- A. 1920cm
- B. 592cm
- C. 296cm
- D. 148cm
- A. 0.040
- B. 0.049
- C. 0.050
- D. 0.49
- B.
- C.
- D.
Correct Answer: Option A
13. Calculate the total surface area of a cupboard which measures 12cm by 10cm by 8cm
Correct Answer: Option B
A = 2((12 x 10) + (10 x 8) + (12 x 8))
A = 2(120 + 80 + 96)
A = 2 x 296
A = 592cm
Answer is B
Explanation
Total surface area of a cupboard is given by the equation A = 2(lb + bh + lh) L = 12, b = 10, h = 8A = 2((12 x 10) + (10 x 8) + (12 x 8))
A = 2(120 + 80 + 96)
A = 2 x 296
A = 592cm
Answer is B
14. Convert 0.04945 to two significant figures
Correct Answer: Option C
15. The probabilities that John and James pass an examination are
respectively. Find the probability of both boys failing the examination.
A.
A.
Correct Answer: Option D
=
x =
Pr(john and james failed)= 1- Pr(john and james passed)
= 1 –
=
Answer is D
B.
1
C.
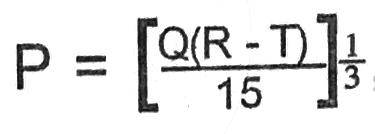
B.
T =
C.
T =R -
D.
T =
B.
C.
D.
21. A machine valued at N20,000 depreciates by 10% every year. What will be the value of the machine at the end of two years?
= x 20000 =18000
At the end of second year, its value = 90% of 18000
= x 18000 = ₦16,200
Answer is A
What is the median mark?
What is the probability of selecting a student from the group that scored 2 or 3
B.
C.
D.
So ₦900 is the cost of
litres
= 14.2857litres of petrol
nbsp; The car uses 1 litre for 14km
So 14.2857 litres will be used for (14.2857 x 14)
= 200km
Answer is D
26
B.
C.
D.
Every 6 months that can be counted on the eight month of the third year is 5
(i.e. 2 times in the first year, 2 times in the second year and once in the third year)
His salary then = initial salary + increment
= 540 + 5(36)
= 540 + 180
= ₦720.00
It can also be solves using a sequence in form of an AP
Answer is C
36. A man stands on a tree 150cm high and sees a boat at an angle of depression of 74°. Find the distance of the boat from the base of the tree.
495g =
= 0.495kg
To express in percentage, 0.495 will be divided by 16.5 and then multiplied by 100
% will be added to the answer
x 100
= 3%
= log 2 23 – log3 9−1
= log2 23 – log3 3−2
Based on law of logarithm
= 3 log2 2 – (-2 log3 3)
But log2 2 = 1,
log3 3 = 1
So, = 3 + 2
= 5
Second quadrant: Sin is positive, Cos is negative and Tan is negative
Third quadrant: Tan is positive, Sin is negative and Cos is negative
Fourth quadrant: Cos is positive, Sin is negative and Tan is negative
The correct option is the third quadrant only where Tanθ is positive and Sinθ is negative
47
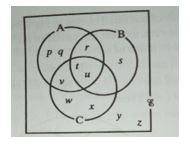
B = (r, s, t, u)
A U B = Elements in both A and B = (p, q, r, s, t, u, v)
(A U B)1 = elements in the universal set E but not in (A U B)= (w, x, y, z)
n(A U B) 1 = number of the elements in (A U B)1 = 4
48. What is the loci of a distance 4cm from a given point P?
Find the value of x
B.
21
C.
32
D.
39
Correct Answer: Option B
So Sin(5x - 28) = Cos(90 - [5x - 28])
Sin(5x - 28) = Cos(90 - 5x + 28)
Sin(5x - 28) = Cos(118 - 5x)………ii
Combining i and ii
Cos(3x - 50) = Cos(118 - 5x)
3x - 50 = 118 - 5x
Collecting the like terms
3x + 5x = 118 + 50
8x = 168
x =
x = 21
Answer is B
Average = sum of numbers / number
=
=
= 15
Explanation
Pr(both John and James passed)=
x =
Pr(john and james failed)= 1- Pr(john and james passed)
= 1 –
=
Answer is D
16. An arc of a
circle of radius 14cm subtends angle 300° at the centre. Find the
perimeter of the sector formed by the arc (take π = )
- A. 14.67cm
- B. 42.67cm
- C. 101.33cm
- D. 513.33cm
17. Simplify
- A. 25
- A.
Correct Answer: Option B
18
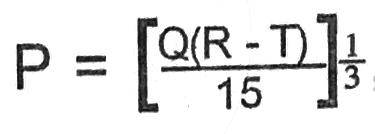
Make T the subject of the relation.
- A. T =
Correct Answer: Option C
19.What is the place value of 9 in the number 3.0492?
- A.
Correct Answer: Option B
20. If the simple interest on a sum of money invested at 3% per annum for 2
years is N123, find the principal.
- A. N676.50
- B. N820
- C. N1,640
- D. N4,920
21. A machine valued at N20,000 depreciates by 10% every year. What will be the value of the machine at the end of two years?
- A. N16,200
- B. N14,200
- C. N12,000
- D. N8,000
Explanation
Since it depreciates by 10% At the end of first year, its value = 90% of 20000= x 20000 =18000
At the end of second year, its value = 90% of 18000
= x 18000 = ₦16,200
Answer is A
22. The table shown gives the marks scored by a group of student in a test. Use the table to answer the question given.
| Mark | 0 | 1 | 2 | 3 | 4 | 5 |
| Frequency | 1 | 2 | 7 | 5 | 4 | 3 |
What is the median mark?
- A. 1
- B. 2
- C. 3
- D. 4
Correct Answer: Option C
Median is the middle number
= Nth2
term = 22th2 = 11th term
Going in ascending order, 11th term is 3, going in descending order 11th term is 3
Median = 3 + 32 = 62 = 3
Answer is C
Explanation
Total frequency = 1 + 2 + 7 + 5 + 4 + 3 = 22Median is the middle number
= Nth2
term = 22th2 = 11th term
Going in ascending order, 11th term is 3, going in descending order 11th term is 3
Median = 3 + 32 = 62 = 3
Answer is C
23. The table shown gives the marks scored by a group of student in a test. Use the table to answer the question given.
| Mark | 0 | 1 | 2 | 3 | 4 | 5 |
| Frequency | 1 | 2 | 7 | 5 | 4 | 3 |
- A.
Correct Answer: Option D
24 A boy walks 800m in 20 minutes. Calculate his average speed in Km/H
- A. 2.4
- B. 4
- C. 24
Correct Answer: Option A
25.A car uses
one litre of petrol for every 14km. If one litre of petrol cost N63.00,
how far can the car go with N900.00 worth of petrol?
- A. 420Km
- B. 405Km
- C. 210Km
- D. 200Km
Explanation
since 1litre cost ₦63So ₦900 is the cost of
litres
= 14.2857litres of petrol
nbsp; The car uses 1 litre for 14km
So 14.2857 litres will be used for (14.2857 x 14)
= 200km
Answer is D
26
- A. 126°
- B. 72°
- C. 54°
-
D.
28°
Correct Answer: Option B
27. How many times, correct to the nearest whole number, will a man run round a circular track of diameter 100m to cover a distance of 1000m?
- A. 3
- B. 4
- C. 5
- D. 6
- A. 35.5
- B. 36.5
- C. 37.5
- D. 38.5
- A. 45.5
- B. 46.5
- C. 47.5
- D. 48.5
- A. 8.8 x 10
- B. 8.8 x 10
- C. 8.8 x 10
- D. 8.8 x 10
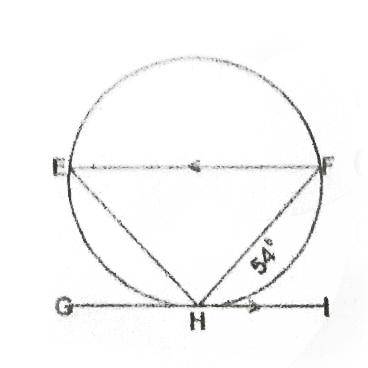
Correct Answer: Option B
Explanation
In terms of distance, a circle has a total distance or perimeter of 2π or πWhere r is radius and D is the diameter
So perimeter =
x 100
= 314.2857m
To cover a distance of 1000m, he is going to round the circular track for
= 3.18
It means it is on the number 4 round after the third round he is going to cover up to 1000m
28

Use the cummulative frequency curve to answer the question. Estimate the median of the date represented on the graph
Correct Answer: Option A
29

Use the cummulative frequency curve to answer the question. What is the 80th percentile?
Correct Answer: Option C
30.
of her share to Taiwo for N720.00. Find the value of the store
- A. N1,080.00
- B. N2,400.00
- C. N3,000.00
- D. N3,600.00
32. A room is
12m long, 9m wide and 8m high. Find the cosine of the angle which a
diagonal of the room makes with the floor of the room
- A.
Correct Answer: Option A
33. Divide the L.C.M of 48, 64 and 80 by their H.C.F
- A. 20
- B. 30
- C. 48
- D. 60
34. Find the equation of the line through (5,7) parallel to the line 7x + 5y = 12
- A. 5x + 7y = 20
- B. 7x + 5y = 70
- C. xy = 7
- D. 15x + 17y = 90
35. A man's
initial salary is N540.00 a month and increases after each period of six
months by N36.00 a month. Find his salary in the eight month of the
third year.
- A. N828.00
- B. N756.00
- C. N720.00
- D. N684.00
Explanation
Since the salary increases by 36 after every 6 monthsEvery 6 months that can be counted on the eight month of the third year is 5
(i.e. 2 times in the first year, 2 times in the second year and once in the third year)
His salary then = initial salary + increment
= 540 + 5(36)
= 540 + 180
= ₦720.00
It can also be solves using a sequence in form of an AP
Answer is C
36. A man stands on a tree 150cm high and sees a boat at an angle of depression of 74°. Find the distance of the boat from the base of the tree.
- A. 52cm
- B. 43cm
- C. 40cm
- D. 15cm
- A. 3x - 2x + x + c
- B. 2x- x+ x + c
- C. 2x– 3x+ c
- D. x+ x– x + c
Correct Answer: Option B
x = 150/tan 74
= 43.01cm
Explanation
Tan 74 = 150/xx = 150/tan 74
= 43.01cm
37. Integrate the expression 6x- 2x + 1
- A. 72
- B. 144
- C. 360
- D. 720
- A. 32cm
- B. 24 cm
- C. 16 cm
- D. 12 cm
- A. 3%
- B. 3 %
- C. 15%
- D. 30%
38. In how many ways can the letters LEADER be arranged?
Correct Answer: Option C
=
= 360
Explanation
The word LEADER has 1L 2E 1A 1D and 1R making total of 6! ==
= 360
39.
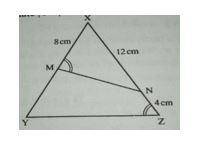
In the figure below, /MX/ = 8cm, /XN/ = 12cm, /NZ/ = 4cm and ∠ XMN = ∠ XZY. Calculate /YM/
Correct Answer: Option C
Explanation
From the figure,∠ XMN = ∠ XZY
Angle X is common
So, ∠ XNM = ∠ XYZ
Then from the angle relationship
= = XM = 8, XZ = 12 + 4 = 16,
XN = 12, XY = 8 + YM
= Cross multiply
8(8 + YM) = 192
64 + 8YM = 192
8YM = 128
YM =
= 16cm
40. Express 495g as a percentage of 16.5kg
Correct Answer: Option A
Explanation
The two numbers must be expressed in the same unit. To convert 495g to kg, it will be divided by 1000495g =
= 0.495kg
To express in percentage, 0.495 will be divided by 16.5 and then multiplied by 100
% will be added to the answer
x 100
= 3%
41. Evaluate (2√3 - 4) (2√3 + 4)
- A. -4
- B. -2
- C. 2
- D. 4
Correct Answer: Option A
= 12 + 8√3 - 8√3 – 16
= 12 – 16
= -4
The two expressions in the bracket are conjugate of each other
Explanation
2√3 - 4) ( 2√3 + 4)= 12 + 8√3 - 8√3 – 16
= 12 – 16
= -4
The two expressions in the bracket are conjugate of each other
42. Find the equation of the tangent at the point (2, 0) to the curve y = x- 2x
- A. y = 2x - 4
- B. y = 2x + 4
- C. y = 2x - 2
- D. y = 2x + 2
Correct Answer: Option A
So 2x - 2
The gradient of the curve is the same with that of the tangent.
At point (2, 0) = 2(2) - 2
= 4 – 2 = 2
The equation of the tangent is given by (y - y1) (x – x1)
At point (x1, y1) = (2, 0)
y - 0 = 2(x - 2)
y = 2x - 4
Explanation
The gradient to the curve is found by differentiating the curve equation with respect to xSo 2x - 2
The gradient of the curve is the same with that of the tangent.
At point (2, 0) = 2(2) - 2
= 4 – 2 = 2
The equation of the tangent is given by (y - y1) (x – x1)
At point (x1, y1) = (2, 0)
y - 0 = 2(x - 2)
y = 2x - 4
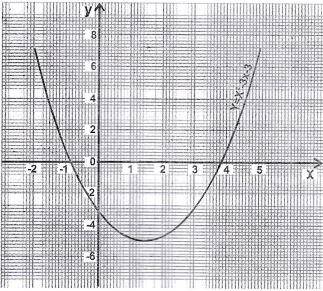
43

Use the quadratic equation curve to answer this questions
What is the 80th percentile?
What is the 80th percentile?
- A. -5.3
- B. 0.5
- C. 3
- D. 8
44. Evaluate log 8 – log
- A. -1 1
- B. -1
- C. 1
- D. 5
Explanation
log2 8 – log3 19= log 2 23 – log3 9−1
= log2 23 – log3 3−2
Based on law of logarithm
= 3 log2 2 – (-2 log3 3)
But log2 2 = 1,
log3 3 = 1
So, = 3 + 2
= 5
45. Tanθ is positive and Sinθ is negative. In which quadrant does θ lies
- A. Second only
- B. Third only
- C. Fourth only
- D. First and third only
Correct Answer: Option B
Explanation
First quadrant: Sin, Cos and Tan are all positiveSecond quadrant: Sin is positive, Cos is negative and Tan is negative
Third quadrant: Tan is positive, Sin is negative and Cos is negative
Fourth quadrant: Cos is positive, Sin is negative and Tan is negative
The correct option is the third quadrant only where Tanθ is positive and Sinθ is negative
Correct Answer: Option B
= 40
Explanation
The total number of students is ∑ f = 3 + 4 + 5 + 6 + 7 + 6 + 5 + 4= 40
47

The figure below is a Venn diagram showing the elements arranged within sets A,B,C,ε.
Use the figure to answer this question
What is n(A U B)1 ?
Use the figure to answer this question
What is n(A U B)1 ?
- A. 2
- B. 3
- C. 4
- D. 7
Correct Answer: Option C
Explanation
A = (p, q, r, t, u, v)B = (r, s, t, u)
A U B = Elements in both A and B = (p, q, r, s, t, u, v)
(A U B)1 = elements in the universal set E but not in (A U B)= (w, x, y, z)
n(A U B) 1 = number of the elements in (A U B)1 = 4
48. What is the loci of a distance 4cm from a given point P?
- A. A straight line of length 4cm
- B. a circle of radius 4cm
- C. perpendicular to point P at 4cm
- D. a circle of diameter 4cm
49. Given that Sin (5
− 28) = Cos(3 − 50), O < 90Find the value of x
- A. 14
Explanation
Sin(5x - 28) = Cos(3x - 50)………..i
But Sinα = Cos(90 - α)So Sin(5x - 28) = Cos(90 - [5x - 28])
Sin(5x - 28) = Cos(90 - 5x + 28)
Sin(5x - 28) = Cos(118 - 5x)………ii
Combining i and ii
Cos(3x - 50) = Cos(118 - 5x)
3x - 50 = 118 - 5x
Collecting the like terms
3x + 5x = 118 + 50
8x = 168
x =
x = 21
Answer is B
50. Find the average of the first four prime numbers greater than 10
- A. 20
- B. 19
- C. 17
- D. 15
Correct Answer: Option D
Explanation
Prime numbers are numbers that has only two factors (i.e 1 and itself). They are numbers that are only divisible by 1 and their selves. First four Prime numbers greater than 10 are 11, 13, 17 and 19Average = sum of numbers / number
=
=
= 15



Comments
Post a Comment